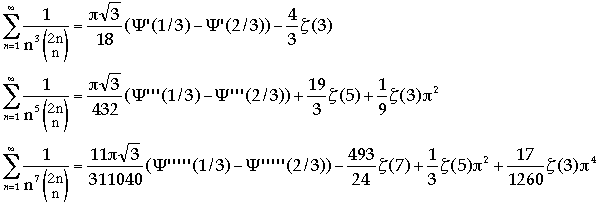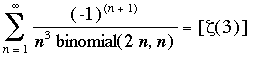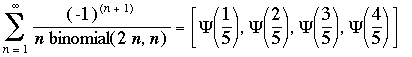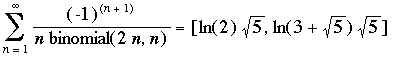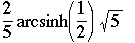Following the first findings that were inspired from Ramanujan Notebooks and other articles, I followed the same idea that the Zeta function (as well as the Psi and Gamma functions) have nice properties. With the help of MapleV, Pari-Gp and my Inverter ,I have found those (new?) identities.