Exact formulas for Integer Sequences

By Simon Plouffe, march 1993

These formulas are all exact and they were found using the author customized bootstrap method. That method is a variant of what is described in [GKP].

The { } denotes the nearest integer function and [ ] the floor function. They were found in 1993. Annnnnn refers to either [Sloane] or [Sloane,Plouffe].

, A000255 is the sequence in of [Sloane], [Sloane,Plouffe] is equal to 1,1,3,11,53,309,2119,16687,148329,1468457,16019531…

, A001339 = 1,3,11,49,261,1631,11743,95901,876809,…

, A001340 = 2,8,38,212,1370,10112,84158,780908…

, A001341 = 6,30,174,1158,8742,74046,696750, …

, A001342 = 24,144,984,7584,65304,…

, A002467 = 0,1,1,4,15,76,455,3186,25487,229384,…

, A000153 = 0,1,2,7,32,181,1214,9403,82508, …

, A000522 = 1,2,5,16,65,326,1957,13700,109601, …

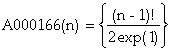, A000166 = 1,0,1,2,9,44,265,1854,14833,133496, …

, A000354 = 1,1,5,29,233,2329,27949,391285, …

, A001540 = 0,2,8,36,184,1110,7776,62216, …

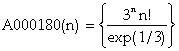, A000180 = 1,2,13,116,1393,20894,376093,7897952, …

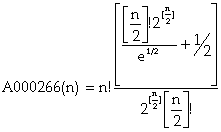, A000266 = 1,1,1,3,15,75,435,3045,24465, …

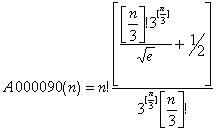, A000090 = 1,1,2,4,16,80,520,3640,29120, …

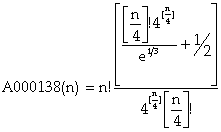, A000138 = 1,1,2,6,18,90,540,3780,31500,…

References :

[AS] Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, 1972.

[GKP] Concrete Mathematics, by Ronald L. Graham, Donald E. Knuth, and Oren Patashnik (Reading, Massachusetts: Addison-Wesley, 1994), xiii+657pp.
ISBN 0-201-55802-5.

[Sloane, Plouffe] The encyclopedia of Integer Sequences, Academic Press, San Diego 600 pp. 1995.

[Sloane N.J.A.] The On-Line Encyclopedia of Integer Sequences.

http://www.research.att.com/~njas/sequences/.