A few identities with Catalan constant and Pi^2

by Simon Plouffe

November 29, 1999

 

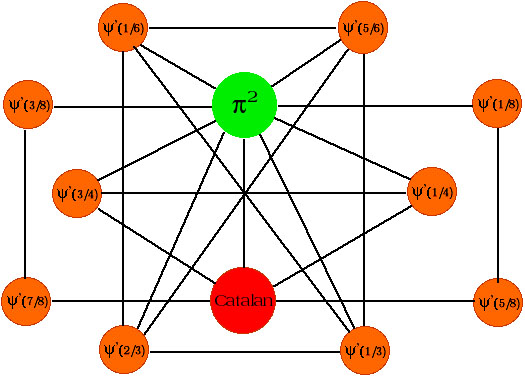
This simple graph represents many of the integer relations with those constants without taking into account the coefficients.

The coefficients can be detected easily with any of the implementation of the LLL or Integer Relation algorithms that exist in many computer algebra programs like Mathematica, Maple or with PSLQ [1]. In this case the coefficients could also be deduced from the numerous functional equations that are known [2].

For example 8*Catalan +Pi^2 - Psi(1,1/4) =0, which is represented by a closed circuit, each closed circuit is an identity (equal to 0). Another example is 16*Pi^2 - 15*Psi(1,2/3) - 3*Psi(1,1/6) = 0. Here Psi(1,x) is the first derivative of the logarithmic derivative of the Gamma function. Another way of saying it : it all comes back to the Gamma function with rational arguments. Of course, this graph does not represent all possible relations with Pi^2, if we add Pi^2 * sqrt(2) the graph gets much more complex. You may consult this computer output for the exact coefficient but I find this graph much easier to read.

 

 

 

A few remarks.

 

There are no known single expression for a number like Psi(1,1/3) alone in terms of Pi^2 and Catalan constant.

 

The identities are symmetric, which comes from the formula Psi(1,x) + Psi(1,1-x) = Pi^2 / sin(Pi*x)^2.

 

Not all the representations of 0 are there, I removed the ones that appear without Pi^2 or Catalan like Psi(1,3/8), Psi(1,7/8) and Psi(1,3/4). There should be with a circuit but since it represents 0 it has to be removed to avoid a false relation with Psi(1,7/8), Psi(1,3/4) and Catalan. The good one is in fact with Psi(1,3/4), Catalan and Pi^2.

 

 

[1] David H. Bailey; Plouffe, Simon, Recognizing numerical constants. Organic mathematics (Burnaby, BC, 1995), 73--88, CMS Conf. Proc., 20, Amer. Math. Soc., Providence, RI, 1997. (Reviewer: Samuel S. Wagstaff, Jr.)

 

[2] L. Lewin, Polylogarithms and Associated Functions, North Holland, New York, 1981. The color of that book is bright orange.